A lens-based ST20 emulator

by Etienne Millon on August 20, 2015

Every year, as part of the SSTIC conference, there is a forensics/reverse engineering challenge. I participated in the 2015 edition. Though I did not manage to complete it, I made an emulator for the exotic ST20 architecture, which is probably worth describing here.

Note that this emulator is not really optimized for pure speed. In the actual challenge I actually had to rewrite it as pure Haskell (i.e., removing the emulation part) so that it was faster. Instead, the goal of this article is to show a few techniques to write powerful emulators in Haskell.

{-# LANGUAGE GeneralizedNewtypeDeriving #-}
{-# LANGUAGE Rank2Types #-}
{-# LANGUAGE TemplateHaskell #-}
import Control.Applicative
import Control.Concurrent
import Control.Monad.RWS
import Control.Lens hiding (imap, op)
import Data.Bits
import Data.Int
import Data.Maybe
import Data.Word
import Numeric
import System.Exit
import System.IO
import Text.Printf

import qualified Data.ByteString as BS
import qualified Data.Map as M
import qualified Data.Set as S

The evaluation monad

This program uses Template Haskell to define lenses, so unfortunately we need to start with a few type definitions.

The ST20’s memory goes from 0x80000000 to 0x7fffffff:

type Address = Int32

We’ll represent the memory using a map. The performance is surprisingly close to that of an array. It is possible to get significantly speeds up memory access by using an IOUArray but it turns loads and stores become monadic operations and makes it impossible to use lenses.

type Mem = M.Map Address Word8

As we’ll see, transputers (hardware threads) can communicate together. We’ll be able to connect it either between them, or to a tty.

data IChannel = InChan (Chan Word8)
              | InHandle Handle

data OChannel = OutChan (Chan Word8)
              | OutHandle Handle

type IChannelMap = [(Int32, IChannel)]
type OChannelMap = [(Int32, OChannel)]

All evaluations take place in a Eval Monad which is a monad transformer stack with the following capabilities:

read and write an EvalState value;
read an EvalEnv value
do some I/O.

newtype Eval a = Eval (RWST EvalEnv () EvalState IO a)
    deriving ( Functor
             , Monad
             , MonadIO
             , MonadReader EvalEnv
             , MonadState EvalState
             )

data EvalEnv =
    EvalEnv
        { envInChans :: IChannelMap
        , envOutChans :: OChannelMap
        }

data EvalState =
    EvalState
        { _iptr :: !Address
        , _intStack :: [Int32]
        , _wptr :: !Int32
        , _mem :: !Mem
        }
$(makeLenses ''EvalState)

runEval :: Mem -> IChannelMap -> OChannelMap -> Eval a -> IO a
runEval memory imap omap (Eval m) =
    fst <$> evalRWST m env st
        where
            env = EvalEnv imap omap
            st =
                 EvalState
                     { _iptr = memStart
                     , _intStack = []
                     , _wptr = 0xaaaaaaaa
                     , _mem = memory
                     }

The above $(...) is a Template Haskell splice. It creates lenses based on the record declaration of EvalState. Lenses are a very powerful tool that makes it possible to compose record reads and updates in a functional way. Here, it defines a lens for each record field; for example, the splice expands to a top-level declaration iptr :: Lens' EvalState Address. But we will define our own lenses too, and everything will remain composable.

Memory

This is naturally adapted to byte access:

memByteOpt :: Address -> Lens' EvalState (Maybe Word8)
memByteOpt addr =
  mem . at addr

See? We composed the mem lens (between an evaluation state and a memory state) with at addr, which is a lens between a memory state and the value at address addr. Well, not exactly: at actually returns a Maybe Word8. We will assume that all memory accesses will succeed, so we want a lens that returns a plain Word8. To achieve this, we can compose with a lens that treats Maybe a as a container of a:

maybeLens :: Lens' (Maybe a) a
maybeLens = lens fromJust (const Just)

memByte :: Address -> Lens' EvalState Word8
memByte addr =
  memByteOpt addr . maybeLens

Sometimes we will also need to access memory word by word. To achieve that, we first define conversion functions.

bytesToWord :: (Word8, Word8, Word8, Word8) -> Int32
bytesToWord (b0, b1, b2, b3) =
    sum [ fromIntegral b0
        , fromIntegral b1 `shiftL` 8
        , fromIntegral b2 `shiftL` 16
        , fromIntegral b3 `shiftL` 24
        ]

wordToBytes :: Int32 -> (Word8, Word8, Word8, Word8)
wordToBytes w =
    (b0, b1, b2, b3)
        where
            b0 = fromIntegral $ w .&. 0x000000ff
            b1 = fromIntegral $ (w .&. 0x0000ff00) `shiftR` 8
            b2 = fromIntegral $ (w .&. 0x00ff0000) `shiftR` 16
            b3 = fromIntegral $ (w .&. 0xff000000) `shiftR` 24

Then, we can define a lens focusing on a 32-bit value.

compose :: [a -> a] -> a -> a
compose = foldr (.) id

get32 :: Address -> EvalState -> Int32
get32 base s =
    bytesToWord (b0, b1, b2, b3)
        where
            b0 = s ^. memByte base
            b1 = s ^. memByte (base + 1)
            b2 = s ^. memByte (base + 2)
            b3 = s ^. memByte (base + 3)

set32 :: Address -> EvalState -> Int32 -> EvalState
set32 base s v =
   compose
       [ set (memByte base) b0
       , set (memByte (base + 1)) b1
       , set (memByte (base + 2)) b2
       , set (memByte (base + 3)) b3
       ] s
        where
            (b0, b1, b2, b3) = wordToBytes v

memWord :: Address -> Lens' EvalState Int32
memWord addr = lens (get32 addr) (set32 addr)

The instruction set reference defines a handy operator to shift an address by a word offset:

(@@) :: Address -> Int32 -> Address
a @@ n = a + 4 * n

It will be also handy to access the memory in list chunks:

mem8s :: Address -> Int32 -> Lens' EvalState [Word8]
mem8s base len = lens getList setList
    where
        getList s =
            map (\ off -> s ^. memByte (base + off)) [0 .. len - 1]
        setList s0 ws =
            compose (zipWith (\ off w -> set (memByte (base + off)) w) [0..] ws) s0

Instruction decoding

Instructions are usually encoded on a single byte: the opcode is in the first nibble, and a parameter is in the second one. For example this is how a LDC (load constant) is encoded:

   .--- 0x40 LDC
  |.---          0x5
  ||
0x45         LDC 0x5

This only works for 4-bytes constants. To load bigger constants, there is a “prefix” operation that will shift the current operand:

   .-------- 0x20 PFX
  |.--------          0x2
  ||
  ||    .--- 0x40 LDC
  ||   |.---          0x5
  ||   ||
0x22 0x45    LDC 0x25

Those are chainable; for example 0x21 0x22 0x45 encodes LDC 0x125.

Another prefix shifts and complements the current operand value:

   .-------- 0x60 NFX
  |.--------          0x2
  ||
  ||    .--- 0x40 LDC
  ||   |.---          0x5
  ||   ||
0x62 0x45    LDC (~0x25)

The ST20 architecture actually provides two type of instructions:

“primary” instructions such as LDC. Their operand is directly encoded.
“secondary” instructions such as MINT (equivalent to LDC 0x80000000). They do not have operands. On the contrary, they are actually a special case of the first type, using a special OPR n opcode. For example, MINT is OPR 0x42, which is encoded using 0x24 0xF2.

We know enough to draft an instruction decoder.

data PInstr = AJW   | ADC
            | LDC   | STL
            | LDL   | LDNL
            | LDLP  | LDNLP
            | CJ    | J
            | EQC   | CALL
            | STNL
    deriving (Eq, Ord, Show)

data SInstr = PROD  | MINT   | GAJW
            | LDPI  | OUT    | IN
            | LB    | XOR    | SB
            | BSUB  | SSUB   | DUP
            | GTx   | WSUB   | AND
            | RET   | GCALL  | SHR
            | SHL   | REM
    deriving (Eq, Ord, Show)

data Instr = Pri PInstr Int32
           | Sec SInstr
    deriving (Eq, Ord)

instance Show Instr where
    show (Pri p n) = show p ++ " " ++ show n
    show (Sec s) = show s

Instruction decoding will need to move within the instruction stream, so it is part of the evaluation monad.

decodeInstr :: Eval Instr
decodeInstr = decodeInstr_ 0

decodeInstr_ :: Int32 -> Eval Instr
decodeInstr_ acc = do
    b <- peekAndIncr
    let acc' = acc + fromIntegral (b .&. 0xf)
    case () of
        _ | b <= 0x0f -> return $ Pri J acc'
        _ | b <= 0x1f -> return $ Pri LDLP acc'
        _ | b <= 0x2f -> decodeInstr_ $ acc' `shiftL` 4
        _ | b <= 0x3f -> return $ Pri LDNL acc'
        _ | b <= 0x4f -> return $ Pri LDC acc'
        _ | b <= 0x5f -> return $ Pri LDNLP acc'
        _ | b <= 0x6f -> decodeInstr_ $ complement acc' `shiftL` 4
        _ | b <= 0x7f -> return $ Pri LDL acc'
        _ | b <= 0x8f -> return $ Pri ADC acc'
        _ | b <= 0x9f -> return $ Pri CALL acc'
        _ | b <= 0xaf -> return $ Pri CJ acc'
        _ | b <= 0xbf -> return $ Pri AJW acc'
        _ | b <= 0xcf -> return $ Pri EQC acc'
        _ | b <= 0xdf -> return $ Pri STL acc'
        _ | b <= 0xef -> return $ Pri STNL acc'
        _             -> return $ Sec $ parseSecondary acc'

peekAndIncr :: Eval Word8
peekAndIncr = do
    addr <- use iptr
    b <- use (memByte addr)
    iptr += 1
    return b

parseSecondary :: Int32 -> SInstr
parseSecondary 0x01 = LB
parseSecondary 0x02 = BSUB
parseSecondary 0x06 = GCALL
parseSecondary 0x07 = IN
parseSecondary 0x08 = PROD
parseSecondary 0x09 = GTx
parseSecondary 0x0a = WSUB
parseSecondary 0x0b = OUT
parseSecondary 0x1b = LDPI
parseSecondary 0x1f = REM
parseSecondary 0x20 = RET
parseSecondary 0x33 = XOR
parseSecondary 0x3b = SB
parseSecondary 0x3c = GAJW
parseSecondary 0x40 = SHR
parseSecondary 0x41 = SHL
parseSecondary 0x42 = MINT
parseSecondary 0x46 = AND
parseSecondary 0x5a = DUP
parseSecondary 0xc1 = SSUB
parseSecondary b = error $ "Unknown secondary 0x" ++ showHex b ""

The two stacks

Data is manipulated using two different mechanisms: the integer stack and the workspace.

The integer stack is a set of three registers: A, B, and C, which can be used as a stack using these operations. Actually, it can only be manipulated through push and pop operations, so we represent this using a list.

The instruction set reference says that an undefined value will be popped if the stack is empty; here we consider that this will not happen, and allow a partial pattern matching.

pushInt :: Int32 -> Eval ()
pushInt n =
    intStack %= (n:)

popInt :: Eval Int32
popInt = do
    (h:t) <- use intStack
    intStack .= t
    return h

popAll :: Eval (Int32, Int32, Int32)
popAll = do
    a <- popInt
    b <- popInt
    c <- popInt
    return (a, b, c)

Only the head (A) can be directly accessed, so we first define a lens between a list and its head, and compose it with intStack.

headLens :: Lens' [a] a
headLens = lens head $ \ l x -> x:tail l

areg :: Lens' EvalState Int32
areg = intStack . headLens

The workspace is a place in memory (pointed to by a register wptr) where local variables can be stored and loaded, a bit like a stack pointer. We first define push and pop operations.

pushWorkspace :: Int32 -> Eval ()
pushWorkspace value = do
    wptr -= 4
    var 0 .= value

popWorkspace :: Eval Int32
popWorkspace = do
    w <- use $ var 0
    wptr += 4
    return w

Then we define a lens to focus on a variable.

var :: Int32 -> Lens' EvalState Int32
var n =
    lens getVar setVar
        where
            varLens s = memWord ((s ^. wptr) @@ n)
            getVar s = s ^. varLens s
            setVar s v = set (varLens s) v s

Input and output

The main particularity of the ST20 architecture is that it has hardware support of message channels. They map fairly naturally to Control.Concurrent.Chan channels. Each ST20 thread will have a map from channel numbers to input or output channels:

getXChan :: (EvalEnv -> [(Int32, a)]) -> Int32 -> EvalEnv -> a
getXChan member w st =
    fromJust $ lookup w $ member st

getIChan :: Int32 -> EvalEnv -> IChannel
getIChan = getXChan envInChans

getOChan :: Int32 -> EvalEnv -> OChannel
getOChan = getXChan envOutChans

And these channels can be either a Chan Word8 or a plain Handle, to connect a thread to the process’ standard input and output.

readFromIChan :: IChannel -> Int32 -> Eval [Word8]
readFromIChan (InChan chan) n =
    liftIO $ mapM (\ _ -> readChan chan) [1..n]
readFromIChan (InHandle h) n =
    liftIO $ do
        bs <- BS.hGet h $ fromIntegral n
        return $ BS.unpack bs

writeToOChan :: OChannel -> [Word8] -> Eval ()
writeToOChan (OutChan chan) ws =
    liftIO $ writeList2Chan chan ws
writeToOChan (OutHandle h) ws =
    liftIO $ do
        BS.hPutStr h $ BS.pack ws
        hFlush h

A few combinators

We first define a few combinators that will help us define the interpret function.

Pop two operands, and push the result:

liftOp :: (Int32 -> Int32 -> Int32) -> Eval ()
liftOp op = do
    a <- popInt
    b <- popInt
    pushInt $ op a b

Exchange two registers:

xchg :: Lens' EvalState Int32 -> Lens' EvalState Int32 -> Eval ()
xchg l1 l2 = do
  x1 <- use l1
  x2 <- use l2
  l1 .= x2
  l2 .= x1

Convert a boolean to an integer:

fromBool :: Bool -> Int32
fromBool False = 0
fromBool True = 1

The `interpret` function

The core of the interpreter is the following function. It takes an instruction and transforms it into a monadic action in Eval.

interpret :: Instr -> Eval ()

Some cases are very simple.

interpret (Pri AJW n) = wptr += 4 * n
interpret (Pri LDNLP n) = areg += 4 * n
interpret (Pri J n) = iptr += n
interpret (Pri LDC n) = pushInt n
interpret (Sec MINT) = pushInt 0x80000000
interpret (Sec GAJW) = xchg areg wptr
interpret (Sec GCALL) = xchg areg iptr
interpret (Pri ADC n) = areg += n
interpret (Pri EQC n) = areg %= (\ a -> fromBool $ a == n)

For some others, we can lift them into the host language and use Haskell operations.

interpret (Sec PROD) = liftOp (*)
interpret (Sec XOR) = liftOp xor
interpret (Sec AND) = liftOp (.&.)
interpret (Sec BSUB) = liftOp (+)
interpret (Sec SSUB) = liftOp $ \ a b -> a + 2 * b
interpret (Sec WSUB) = liftOp (@@)
interpret (Sec GTx) = liftOp $ \ a b -> fromBool $ b > a
interpret (Sec SHR) = liftOp $ \ a b -> b `shiftR` fromIntegral a
interpret (Sec SHL) = liftOp $ \ a b -> b `shiftL` fromIntegral a
interpret (Sec REM) = liftOp $ \ a b -> b `mod` a

Others need a few operations to prepare the operands and access memory.

interpret (Sec SB) = do
    a <- popInt
    b <- popInt
    memByte a .= fromIntegral b
interpret (Sec DUP) = do
    a <- popInt
    pushInt a
    pushInt a
interpret (Pri STL n) = do
    v <- popInt
    var n .= v
interpret (Pri LDLP n) = do
    v <- use wptr
    pushInt $ v @@ n
interpret (Pri LDL n) = do
    v <- use $ var n
    pushInt v
interpret (Sec LDPI) = do
    ip <- use iptr
    areg += ip
interpret (Pri CJ n) = do
    a <- popInt
    let d = if a == 0 then n else 0
    iptr += d
interpret (Sec LB) = do
    a <- use areg
    a' <- fromIntegral <$> use (memByte a)
    areg .= a'
interpret (Pri STNL n) = do
    a <- popInt
    b <- popInt
    memWord (a @@ n) .= b
interpret (Pri LDNL n) = do
    a <- use areg
    a' <- use $ memWord $ a @@ n
    areg .= a'

Call and return instructions use the workspace to pass arguments.

interpret (Pri CALL n) = do
    (a, b, c) <- popAll
    pushWorkspace c
    pushWorkspace b
    pushWorkspace a
    ip <- use iptr
    pushWorkspace ip
    areg .= ip
    iptr += n
interpret (Sec RET) = do
    newIp <- popWorkspace
    _ <- popWorkspace
    _ <- popWorkspace
    _ <- popWorkspace
    iptr .= newIp

To perform I/O, the calling transputer needs to supply three things in the int stack:

the number of bytes to transfer;
a pointer to a channel;
where to read or write the message.

The channel itself is abstracted in the transputer’s channel maps. Most reads succeed; however the first transputer’s channel 0 will read directly from a file, so it will reach end of file at some time. We can detect that when an empty list is read, and exit the process.

interpret (Sec OUT) = do
    (len, pChan, pMsg) <- popAll
    message <- use $ mem8s pMsg len
    chan <- asks $ getOChan pChan
    writeToOChan chan message
interpret (Sec IN) = do
    (len, pChan, pMsg) <- popAll
    chan <- asks $ getIChan pChan
    input <- readFromIChan chan len
    when (null input) $ liftIO exitSuccess
    mem8s pMsg (fromIntegral $ length input) .= input

The core of the interpreter is then very simple:

evalLoop :: Eval ()
evalLoop = do
    i <- decodeInstr
    interpret i
    evalLoop

Boot from link

Several things are missing: the memory map, and how the system boots.

It turns out that the ST20 has a very simple boot protocol:

read 1 byte from port 0, call it n
read n bytes from port 0
store those at memStart
set the workspace just after this memory chunk
jump to memStart

bootSeq :: Eval ()
bootSeq = do
    chan <- asks $ getIChan $ iPin 0
    len <- head <$> readFromIChan chan 1
    prog <- readFromIChan chan $ fromIntegral len
    mem8s memStart (fromIntegral $ length prog) .= prog
    wptr .= memStart + fromIntegral len

There’s some flexibility on memStart, but this value works:

memStart :: Address
memStart = 0x80000100

Pin numbers, however, are mapped to fixed address:

iPin :: Int32 -> Int32
iPin n = 0x80000010 @@ n

oPin :: Int32 -> Int32
oPin n = 0x80000000 @@ n

We decide to initialize the memory with zeroes:

initialMem :: Mem
initialMem =
    M.fromList $ zip [0x80000000 .. memEnd] $ repeat 0
        where
            memSize = 0x4000
            memEnd = memStart + memSize - 1

Booting a transputer is then just a matter of reading from the correct channel and doing the rest of the evaluation loop.

transputer :: Maybe Analysis
           -> [((Int32, IChannel), (Int32, OChannel))]
           -> IO (MVar ())
transputer analysis cmap = do
    let (imap, omap) = unzip cmap
    fork $ runEval initialMem imap omap $ do
        bootSeq
        runAnalysis analysis
        evalLoop

Multithreading boilerplate

If you fork threads and don’t wait for them, nothing will happen since the main thread will just exit. The solution is to create a “control” MVar that will be signalled to by each thread:

fork :: IO () -> IO (MVar ())
fork io = do
    mvar <- newEmptyMVar
    _ <- forkFinally io $ \ _ -> putMVar mvar ()
    return mvar

And to wait for all of them:

runAll :: [IO (MVar ())] -> IO ()
runAll ms = do
    threads <- sequence ms
    mapM_ takeMVar threads

Connecting the lines

For this problem we have 13 transputers.

data TransputerName = T00 | T01 | T02 | T03
                    | T04 | T05 | T06 | T07
                    | T08 | T09 | T10 | T11
                    | T12
  deriving (Enum, Eq)

We devise a way to connect them together. The communication between two transputers is bidirectional, so we need two channels. Each of them is converted to an OChannel on one side and an IChannel on the other one.

connect :: TransputerName -> Int32
        -> TransputerName -> Int32
        -> IO [(TransputerName, Int32, OChannel, IChannel)]
connect src srcPort dst dstPort = do
  x <- newChan
  y <- newChan
  return [ (src, srcPort, OutChan x, InChan y)
         , (dst, dstPort, OutChan y, InChan x)
         ]

Booting them is a matter of creating the correct communication channels (this pinout list comes from a schematic that was present in the challenge files).

main :: IO ()
main = do
    pins <- concat <$> sequence
        [ connect T00 1 T01 0
        , connect T00 2 T02 0
        , connect T00 3 T03 0
        , connect T01 1 T04 0
        , connect T01 2 T05 0
        , connect T01 3 T06 0
        , connect T02 1 T07 0
        , connect T02 2 T08 0
        , connect T02 3 T09 0
        , connect T03 1 T10 0
        , connect T03 2 T11 0
        , connect T03 3 T12 0
        , connect T11 1 T12 1
        ]
    runAll $ map (buildTransputer pins) [T00 ..]
        where
            buildTransputer pins t =
                transputer (isDebug t) $ onlyFor t pins ++ extraPins t
            pin n ochan ichan = ((iPin n, ichan), (oPin n, ochan))
            onlyFor src l = [pin p oc ic | (name, p, oc, ic) <- l, name == src]
            extraPins T00 = [((iPin 0, InHandle stdin), (oPin 0, OutHandle stdout))]
            extraPins _ = []

Bonus: static analysis tools

The above transputer function is controlled by the following configuration:

data Analysis = Graph | Disasm

isDebug :: TransputerName -> Maybe Analysis
isDebug _ = Nothing

It means that for each transputer, we can choose to print a graph or a disassembly of the code that will be executed. To do that, we will first compute the set of all edges in the control flow graph.

This analysis relies on a nextInstr function that statically computes the set of next instructions. These can be reached either because it’s the next one in the instruction flow (DSeq), because of jump (DJmp), or an unknown destination, for example after a RET (DDyn).

data Dest = DSeq Address
          | DJmp Address
          | DDyn
    deriving (Eq, Ord)

nextInstrs :: Instr -> [Dest]
nextInstrs (Pri CJ n) = [DSeq 0, DJmp n]
nextInstrs (Pri J n) = [DJmp n]
nextInstrs (Pri CALL n) = [DSeq 0, DJmp n]
nextInstrs (Sec GCALL) = [DDyn]
nextInstrs (Sec RET) = [DDyn]
nextInstrs _ = [DSeq 0]

We can wrap this function in a monadic one that can turn these relative addresses into absolute ones (since it can know the addresses of functions).

type EdgeSet = S.Set (Address, Instr, Dest)

instrDests :: Address -> Eval EdgeSet
instrDests start = do
    iptr .= start
    i <- decodeInstr
    let deltaips = nextInstrs i
    new <- use iptr
    return $ S.fromList $ map (\ d -> (start, i, adjust new d)) deltaips
        where
            adjust n (DSeq d) = DSeq $ n + d
            adjust n (DJmp d) = DJmp $ n + d
            adjust _ DDyn = DDyn

Then, the algorithm consists in computing the fixpoint of the following iterating function:

step :: EdgeSet -> Eval EdgeSet
step s = do
    xs <- mapM (basicBlockM . getDest) $ S.toList s
    return $ S.union s $ S.unions xs
        where
            getDest (_, _, DSeq a) = Just a
            getDest (_, _, DJmp a) = Just a
            getDest (_, _, DDyn) = Nothing
            basicBlockM (Just a) = instrDests a
            basicBlockM Nothing = return S.empty

The fixpoint itself is computed using the following function, which takes a predicate on two EdgeSets to stop the iteration.

stepUntil :: ((EdgeSet, EdgeSet) -> Bool) -> (EdgeSet, EdgeSet) -> Eval EdgeSet
stepUntil p (a, b) | p (a, b) = return b
stepUntil p (_, b) = do
    c <- step b
    stepUntil p (b, c)

We’ll stop when their size is equal.

runAnalysis :: Maybe Analysis -> Eval ()
runAnalysis Nothing = return ()
runAnalysis (Just analysis) = do
    s0 <- instrDests memStart
    let p (a, b) = S.size a == S.size b
    r <- stepUntil p (S.empty, s0)
    liftIO $ putStrLn $ convert analysis r
    iptr .= memStart

Finally, here is how to convert the EdgeSets in a human-readable form.

convert :: Analysis -> EdgeSet -> String
convert Graph es =
    "digraph G{\n"
    ++ "node[shape=point]\n"
    ++ concatMap edge (S.toList es)
    ++ "}"
        where
            edge (x, i, y) = show x ++ " -> " ++ toNode x y ++ "[label=\"" ++ show i ++ "\"];\n"
            toNode _ (DSeq a) = show a
            toNode _ (DJmp a) = show a
            toNode x DDyn = "dyn" ++ show x
convert Disasm es = concatMap go $ S.toList es
    where
        go (x, i, DSeq _) =
            printf "%04x %s\n" x (show i)
        go (x, i, DJmp y) =
            printf "%04x %s  [* %04x]\n" x (show i) y
        go (x, i, DDyn) =
            printf "%04x %s  [* dyn]\n" x (show i)

For example here is an extract of the beginning of the first transputer. You can notice instructions with several destinations (conditional jumps) are displayed twice.

80000100 AJW -76
80000102 LDC 0
80000103 STL 1
80000104 LDC 0
80000105 STL 3
80000106 MINT
80000108 LDNLP 1024
8000010b GAJW
8000010d AJW -76
8000010f LDC 201
80000111 LDPI
80000113 MINT
80000115 LDC 8
80000116 OUT
80000117 LDLP 73
80000119 MINT
8000011b LDNLP 4
8000011c LDC 12
8000011d IN
8000011e LDL 73
80000120 CJ 21
80000120 CJ 21  [* 80000137]
80000122 LDC 205
80000124 LDPI

For the graph output, I assume that you have already seen graphviz output:

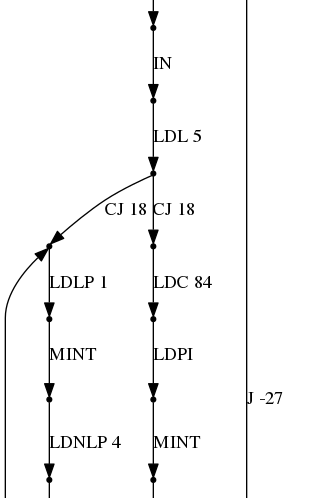
The introduction image was done using the same output but an alternative layout engines.

Hope you enjoyed this article!

Enter the void *